Introduction
Mathematics is used by engineers to solve problems. This usually involves developing a mathematical model. Just as when building a working model aeroplane we would hope to include all the important features, the same thing applies when building a mathematical model. We would also like to indicate the things we have had to leave out because they were too fiddly to deal with, and also those details that we think are irrelevant to the model. In the case of a mathematical model the things that have been left out are listed under assumptions of the model. To build a mathematical model, we usually need to use scientific rules about the way things in the world behave (e.g. Newton’s laws of motion, conservation of momentum and energy, Ohm’s law, Kirchoff’s laws for circuits, etc.) and use numbers, variables, equations, and inequalities to express the problem in a mathematical language.
Some problems are very easy to describe mathematically. For instance: ‘Three people sitting in a room were joined by two others, how many people are there in the room in total?’ This can be described by the sum 3 + 2 =? and can be solved easily as 3 + 2 = 5.
The final stage of solving the problem is to translate it back into the original setting – the answer is: ‘there are 5 people in the room in total’.
Assumptions were used to solve this problem. We assumed that noone else came in or left the room in the meantime and we made general assumptions about the stability of the room, for example, the building containing it did not fall down. However, these assumptions are so obvious that they do not need to be listed. In more complex problems it is necessary to list important assumptions as they may have relevance as to the validity of the solution.
Another example is as follows: ‘There are three resistors in series in a circuit, two of the resistors are known to have resistance of 3 and 4 ohm, respectively. The voltage source is a battery of 12 V and the current is measured as 1 A. What is the resistance of the third resistor?’
To help express the problem in a mathematical form we may draw a circuit diagram as in Figure 1:
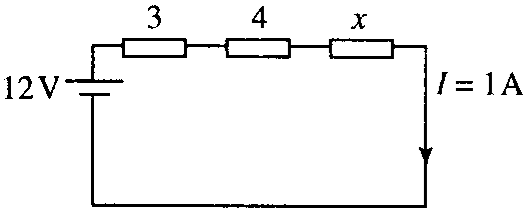
The problem can be expressed mathematically by using Ohm’s law and the fact that an equivalent resistance to resistances in series is given by the sum of the individual resistances. If x is the unknown value of the third resistance and V = RI where R = R1 + R2 + R3, we obtain:
12 = (3 + 4 + x)1
The expression of the mathematical problem has taken the form of an equation where we now need to find x, the value of the third resistance. The main assumptions that have been used to build this mathematical model are:
- There are such things as pure resistors that have no capacitance or inductance.
- Resistances remain constant and are not affected by any possible temperature changes or other environmental effects.
- The battery gives a constant voltage that does not deteriorate with time.
- The battery introduces no resistance to the circuit.
These assumptions are simplifications that are acceptable because although the real world cannot behave with the simplicity of the mathematical model, the amount of error introduced by making these assumptions is small.
Once we have the solution of a mathematical model then it should be tested against a real-life situation to see whether the model behaves reasonably closely to reality. Once the model has been accepted then it can be used to predict the behaviour of the system for input values other than those that it has been tested for.
The stages in solving a problem are as follows:
- Take to real problem and express it as a mathematical one using any necessary scientific rules and assumptions about the behaviour of the system and using letters to represent any unknown quantities. Include an account of any important assumptions and simplifications made.
- Solve the mathematical problem using your knowledge of mathematics.
- Translate the mathematical solution back into the setting of your original problem.
- Test the model solutions for some values to check that it behaves like the real-life problem.
Most mathematical problems are expressed by using equations, or inequalities, differential or difference equations, or by expressing a problem geometrically or a combination of all of these. We might need to incorporate a random element which results in the need to use a probabilistic model. We can take a look at the modelling process in more detail as we come across new mathematical tools and the situations in which they are used. To perform the entire modelling cycle properly, we need to be able to test our results in a real-life situation in order to reconsider assumptions used in the model. This would require access to engineering situations and tools. Many of the applied problems however do present an opportunity to move from an English language description of a problem to a mathematical language description of a problem, which is an important step in the modelling process.
To solve the problem using your knowledge of mathematics, we need to use the ideas of mathematical statements and how to decide whether, and express the fact that, one statement leads logically on to the next. We shall use examples of solving equations and inequalities although the same ideas apply to the solving of all problems.
Describing a problem in mathematical language
The stages in expressing a problem in mathematical language can be summarized as:
- Assign letters to represent the unknown quantities.
- Write down the known facts using equations and inequalities, and using drawings and diagrams where necessary.
- Express the problem to be solved mathematically.
This is not a simple process because it involves a great deal of interpretation of the original problem. It is useful to try to limit the number of unknowns used as much as possible, or the problem may appear more difficult than necessary.
To be continued…